如何用C语言画一个“圣诞树”?
时间:2016-12-25 10:44 点击:次
我使用了左右镜像的Sierpinski triangle,每层减去上方一小块,再用符号点缀。可生成不同层数的「圣诞树」,如下图是5层的结果。
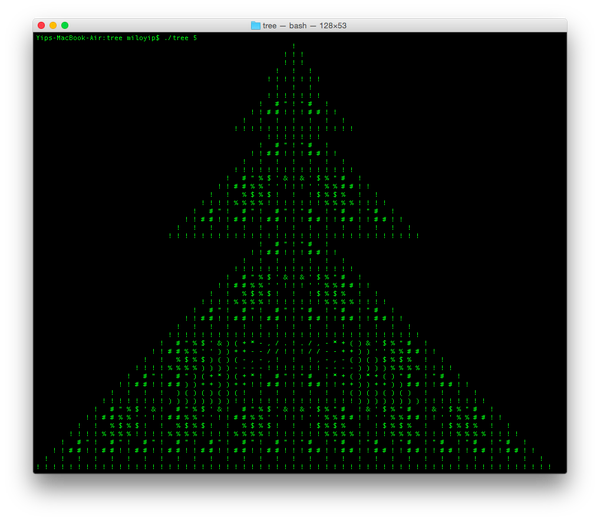
基本代码来自Sierpinski triangle的实现,字符的想法来自于code golf - Draw A Sierpinski Triangle。
--
更新1: 上面的是我尝试尽量用最少代码来画一个抽象一点的圣诞树,因此树干都没有。然后,我尝试用更真实一点的风格。因为树是一个比较自相似的形状,这次使用递归方式描述树干和分支。
n = 0的时候,就是只画一主树干,树干越高就越幼:
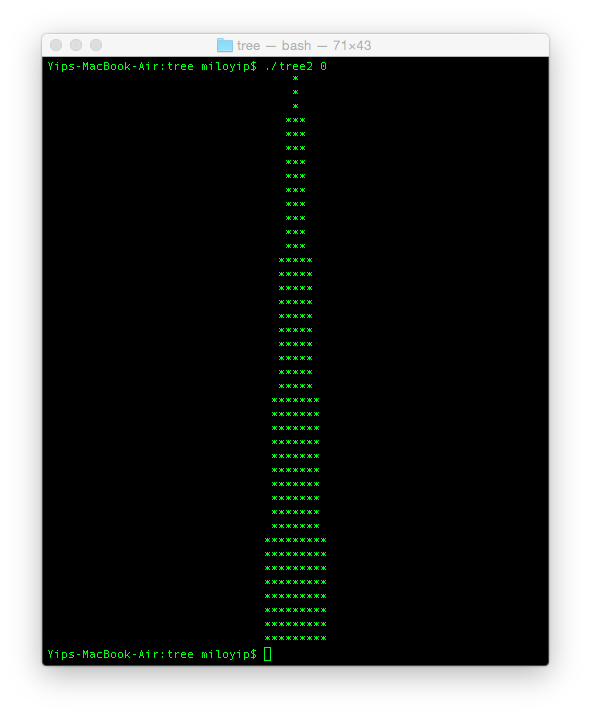
n = 1的时候,利用递归画向两面分支,旋转,越高的部分缩得越小。
 n = 2 的时候,继续分支出更细的树支。
n = 2 的时候,继续分支出更细的树支。
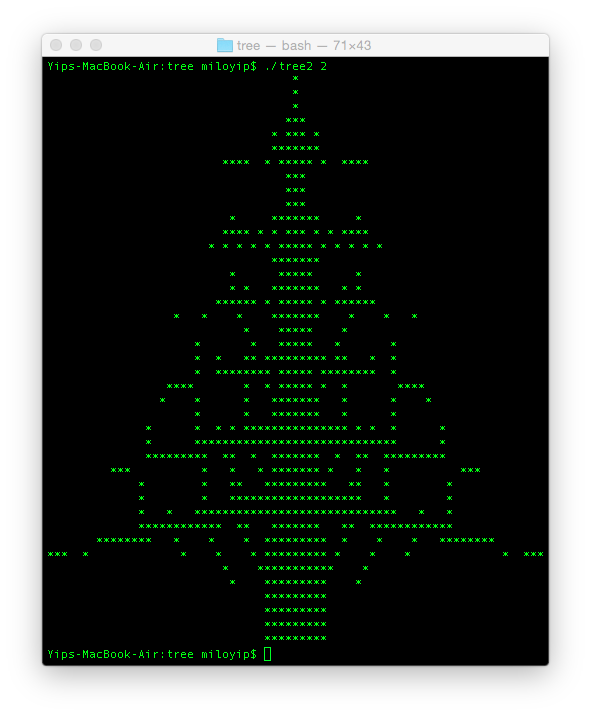 n = 3就差不多够细节了。
n = 3就差不多够细节了。
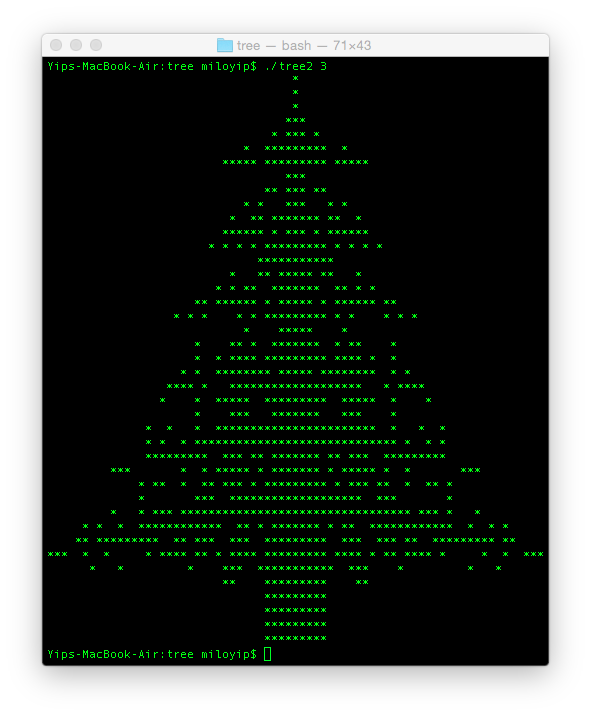 代码长一点,为了容易理解我不「压缩」它了。
代码长一点,为了容易理解我不「压缩」它了。
这段代码实际上是用了圆形的距离场来建模,并且没有优化。
这是一棵「祼树」,未能称得上是「圣诞树」。
--
更新2: 简单地加入装饰及丝带,在命令行可以选择放大倍率,下图是两倍大的。

2D的我想已差不多了。接下来看看有没有空尝试3D的。
--
更新3:终于要3D了。之前每个节点是往左和右分支,在三维中我们可以更自由一点,我尝试在每个节点申出6个分支。最后用了简单的Lambertian着色(即max(dot(N, L), 0)。
n = 1 的时候比较容易看出立体的着色:

可是n=3的时候已乱得难以辨认:

估计是因为aliasing而做成的。由于光照已经使用了finite difference来计算法线,性能已经很差,我就不再尝试做Supersampling去解决aliasing的问题了。另外也许Ambient occlusion对这问题也有帮助,不过需要更多的采样。
因为需要三维旋转,不能像二维简单使用一个角度来代表旋转,所以这段代码加入了不少矩阵运算。当然用四元数也是可以的。
--
更新4:发现之前的TransformLength()写错了,上面已更正。另外,考虑提升性能时,一般是需要一些空间剖分的方式去加速检查,但这里刚好是一个树状的场景结构,可以简单使用Bounding volume hierarchy,我使用了球体作为包围体积。只需加几句代码,便可以大大缩减运行时间。
另外,考虑到太小的叶片是很难采样得到好看的结果,我尝试以一个较大的球体去表现叶片(就如素描时考虑更整体的光暗而不是每片叶片的光暗),我觉得结果有进步。


#include <stdio.h>
#include <stdlib.h>
int main(int argc, char* argv[]) {
int n = argc > 1 ? atoi(argv[1]) : 4;
for (int j = 1; j <= n; j++) {
int s = 1 << j, k = (1 << n) - s, x;
for (int y = s - j; y >= 0; y--, putchar('\n')) {
for (x = 0; x < y + k; x++) printf(" ");
for (x = 0; x + y < s; x++) printf("%c ", '!' ^ y & x);
for (x = 1; x + y < s; x++) printf("%c ", '!' ^ y & (s - y - x - 1));
}
}
}
基本代码来自Sierpinski triangle的实现,字符的想法来自于code golf - Draw A Sierpinski Triangle。
--
更新1: 上面的是我尝试尽量用最少代码来画一个抽象一点的圣诞树,因此树干都没有。然后,我尝试用更真实一点的风格。因为树是一个比较自相似的形状,这次使用递归方式描述树干和分支。
n = 0的时候,就是只画一主树干,树干越高就越幼:

n = 1的时候,利用递归画向两面分支,旋转,越高的部分缩得越小。
 n = 2 的时候,继续分支出更细的树支。
n = 2 的时候,继续分支出更细的树支。 n = 3就差不多够细节了。
n = 3就差不多够细节了。 代码长一点,为了容易理解我不「压缩」它了。
代码长一点,为了容易理解我不「压缩」它了。
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define PI 3.14159265359
float sx, sy;
float sdCircle(float px, float py, float r) {
float dx = px - sx, dy = py - sy;
return sqrtf(dx * dx + dy * dy) - r;
}
float opUnion(float d1, float d2) {
return d1 < d2 ? d1 : d2;
}
#define T px + scale * r * cosf(theta), py + scale * r * sin(theta)
float f(float px, float py, float theta, float scale, int n) {
float d = 0.0f;
for (float r = 0.0f; r < 0.8f; r += 0.02f)
d = opUnion(d, sdCircle(T, 0.05f * scale * (0.95f - r)));
if (n > 0)
for (int t = -1; t <= 1; t += 2) {
float tt = theta + t * 1.8f;
float ss = scale * 0.9f;
for (float r = 0.2f; r < 0.8f; r += 0.1f) {
d = opUnion(d, f(T, tt, ss * 0.5f, n - 1));
ss *= 0.8f;
}
}
return d;
}
int main(int argc, char* argv[]) {
int n = argc > 1 ? atoi(argv[1]) : 3;
for (sy = 0.8f; sy > 0.0f; sy -= 0.02f, putchar('\n'))
for (sx = -0.35f; sx < 0.35f; sx += 0.01f)
putchar(f(0, 0, PI * 0.5f, 1.0f, n) < 0 ? '*' : ' ');
}
这是一棵「祼树」,未能称得上是「圣诞树」。
--
更新2: 简单地加入装饰及丝带,在命令行可以选择放大倍率,下图是两倍大的。

// f() 及之前的部分沿上
int ribbon() {
float x = (fmodf(sy, 0.1f) / 0.1f - 0.5f) * 0.5f;
return sx >= x - 0.05f && sx <= x + 0.05f;
}
int main(int argc, char* argv[]) {
int n = argc > 1 ? atoi(argv[1]) : 3;
float zoom = argc > 2 ? atof(argv[2]) : 1.0f;
for (sy = 0.8f; sy > 0.0f; sy -= 0.02f / zoom, putchar('\n'))
for (sx = -0.35f; sx < 0.35f; sx += 0.01f / zoom) {
if (f(0, 0, PI * 0.5f, 1.0f, n) < 0.0f) {
if (sy < 0.1f)
putchar('.');
else {
if (ribbon())
putchar('=');
else
putchar("............................#j&o"[rand() % 32]);
}
}
else
putchar(' ');
}
}
2D的我想已差不多了。接下来看看有没有空尝试3D的。
--
更新3:终于要3D了。之前每个节点是往左和右分支,在三维中我们可以更自由一点,我尝试在每个节点申出6个分支。最后用了简单的Lambertian着色(即max(dot(N, L), 0)。
n = 1 的时候比较容易看出立体的着色:

可是n=3的时候已乱得难以辨认:

估计是因为aliasing而做成的。由于光照已经使用了finite difference来计算法线,性能已经很差,我就不再尝试做Supersampling去解决aliasing的问题了。另外也许Ambient occlusion对这问题也有帮助,不过需要更多的采样。
因为需要三维旋转,不能像二维简单使用一个角度来代表旋转,所以这段代码加入了不少矩阵运算。当然用四元数也是可以的。
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define PI 3.14159265359f
float sx, sy;
typedef float Mat[4][4];
typedef float Vec[4];
void scale(Mat* m, float s) {
Mat temp = { {s,0,0,0}, {0,s,0,0 }, { 0,0,s,0 }, { 0,0,0,1 } };
memcpy(m, &temp, sizeof(Mat));
}
void rotateY(Mat* m, float t) {
float c = cosf(t), s = sinf(t);
Mat temp = { {c,0,s,0}, {0,1,0,0}, {-s,0,c,0}, {0,0,0,1} };
memcpy(m, &temp, sizeof(Mat));
}
void rotateZ(Mat* m, float t) {
float c = cosf(t), s = sinf(t);
Mat temp = { {c,-s,0,0}, {s,c,0,0}, {0,0,1,0}, {0,0,0,1} };
memcpy(m, &temp, sizeof(Mat));
}
void translate(Mat* m, float x, float y, float z) {
Mat temp = { {1,0,0,x}, {0,1,0,y}, {0,0,1,z}, {0,0,0,1} };
memcpy(m, &temp, sizeof(Mat));
}
void mul(Mat* m, Mat a, Mat b) {
Mat temp;
for (int j = 0; j < 4; j++)
for (int i = 0; i < 4; i++) {
temp[j][i] = 0.0f;
for (int k = 0; k < 4; k++)
temp[j][i] += a[j][k] * b[k][i];
}
memcpy(m, &temp, sizeof(Mat));
}
void transformPosition(Vec* r, Mat m, Vec v) {
Vec temp = { 0, 0, 0, 0 };
for (int j = 0; j < 4; j++)
for (int i = 0; i < 4; i++)
temp[j] += m[j][i] * v[i];
memcpy(r, &temp, sizeof(Vec));
}
float transformLength(Mat m, float r) {
return sqrtf(m[0][0] * m[0][0] + m[0][1] * m[0][1] + m[0][2] * m[0][2]) * r;
}
float sphere(Vec c, float r) {
float dx = c[0] - sx, dy = c[1] - sy;
float a = dx * dx + dy * dy;
return a < r * r ? sqrtf(r * r - a) + c[2] : -1.0f;
}
float opUnion(float z1, float z2) {
return z1 > z2 ? z1 : z2;
}
float f(Mat m, int n) {
float z = -1.0f;
for (float r = 0.0f; r < 0.8f; r += 0.02f) {
Vec v = { 0.0f, r, 0.0f, 1.0f };
transformPosition(&v, m, v);
z = opUnion(z, sphere(v, transformLength(m, 0.05f * (0.95f - r))));
}
if (n > 0) {
Mat ry, rz, s, t, m2, m3;
rotateZ(&rz, 1.8f);
for (int p = 0; p < 6; p++) {
rotateY(&ry, p * (2 * PI / 6));
mul(&m2, ry, rz);
float ss = 0.45f;
for (float r = 0.2f; r < 0.8f; r += 0.1f) {
scale(&s, ss);
translate(&t, 0.0f, r, 0.0f);
mul(&m3, s, m2);
mul(&m3, t, m3);
mul(&m3, m, m3);
z = opUnion(z, f(m3, n - 1));
ss *= 0.8f;
}
}
}
return z;
}
float f0(float x, float y, int n) {
sx = x;
sy = y;
Mat m;
scale(&m, 1.0f);
return f(m, n);
}
int main(int argc, char* argv[]) {
int n = argc > 1 ? atoi(argv[1]) : 3;
float zoom = argc > 2 ? atof(argv[2]) : 1.0f;
for (float y = 0.8f; y > -0.0f; y -= 0.02f / zoom, putchar('\n'))
for (float x = -0.35f; x < 0.35f; x += 0.01f / zoom) {
float z = f0(x, y, n);
if (z > -1.0f) {
float nz = 0.001f;
float nx = f0(x + nz, y, n) - z;
float ny = f0(x, y + nz, n) - z;
float nd = sqrtf(nx * nx + ny * ny + nz * nz);
float d = (nx - ny + nz) / sqrtf(3) / nd;
d = d > 0.0f ? d : 0.0f;
// d = d < 1.0f ? d : 1.0f;
putchar(".-:=+*#%@@"[(int)(d * 9.0f)]);
}
else
putchar(' ');
}
}
更新4:发现之前的TransformLength()写错了,上面已更正。另外,考虑提升性能时,一般是需要一些空间剖分的方式去加速检查,但这里刚好是一个树状的场景结构,可以简单使用Bounding volume hierarchy,我使用了球体作为包围体积。只需加几句代码,便可以大大缩减运行时间。
另外,考虑到太小的叶片是很难采样得到好看的结果,我尝试以一个较大的球体去表现叶片(就如素描时考虑更整体的光暗而不是每片叶片的光暗),我觉得结果有进步。

float f(Mat m, int n) {
// Culling
{
Vec v = { 0.0f, 0.5f, 0.0f, 1.0f };
transformPosition(&v, m, v);
if (sphere(v, transformLength(m, 0.55f)) == -1.0f)
return -1.0f;
}
float z = -1.0f;
if (n == 0) { // Leaf
Vec v = { 0.0f, 0.5f, 0.0f, 1.0f };
transformPosition(&v, m, v);
z = sphere(v, transformLength(m, 0.3f));
}
else { // Branch
for (float r = 0.0f; r < 0.8f; r += 0.02f) {
Vec v = { 0.0f, r, 0.0f, 1.0f };
transformPosition(&v, m, v);
z = opUnion(z, sphere(v, transformLength(m, 0.05f * (0.95f - r))));
}
}
// ...
}
本文章来源于知乎,作者Milo Yip
顶一下
(14)
100%
踩一下
(0)
0%
上一篇:C语言核心之数组和指针详解
相关内容:
 QQ群
QQ群
-
 微信
微信

-
 返回首页
返回首页 -
 返回顶部
返回顶部



