C++函数的嵌套调用

时间：2014-10-15 14:50 点击：次

C++不允许对函数作嵌套定义，也就是说在一个函数中不能完整地包含另一个函数。在一个程序中每一个函数的定义都是互相平行和独立的。

虽然C++不能嵌套定义函数，但可以嵌套调用函数，也就是说，在调用一个函数的过程中，又调用另一个函数。

在程序中实现函数嵌套调用时，需要注意的是：在调用函数之前，需要对每一个被调用的函数作声明(除非定义在前，调用在后)。

【例4.9】用弦截法求方程f(x)=x3-5x2+16x-80=0的根。

这是一个数值求解问题，需要先分析用弦截法求根的算法。根据数学知识，可以列出以下的解题步骤：
1) 取两个不同点x1，x2，如果f(x1)和f(x2)符号相反，则(x1，x2)区间内必有一个根。如果f(x1)与f(x2)同符号，则应改变 x1，x2，直到f(x1)， f(x2)异号为止。注意x1､x2的值不应差太大，以保证(x1，x2)区间内只有一个根。

2) 连接(x1， f(x1))和(x2， f(x2))两点，此线(即弦)交x轴于x，见图4.7。

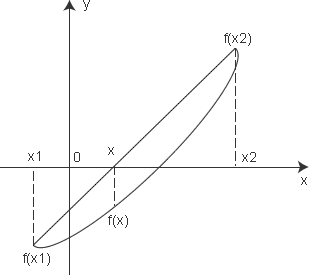
图 4.7

x点坐标可用下式求出：

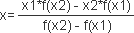
再从x求出f(x)。

3) 若f(x)与f(x1)同符号，则根必在(x， x2)区间内，此时将x作为新的x1。如果f(x)与f(x2)同符号，则表示根在( x1，x)区间内，将x作为新的x2。

4) 重复步骤 (2) 和 (3)，直到 |f(x)|<ξ为止， ξ为一个很小的正数，例如10^-6。此时认为 f(x)≈0。

这就是弦截法的算法，在程序中分别用以下几个函数来实现以上有关部分功能：
1) 用函数f(x)代表x的函数:x3-5x2+16x-80。

2) 用函数xpoint (x1,x2)来求(x1,f(x1))和(x2,f(x2))的连线与x轴的交点x的坐标。

3) 用函数root(x1,x2)来求(x1,x2)区间的那个实根。显然，执行root函数的过程中要用到xpoint函数，而执行xpoint函数的过程中要用到f函数。

根据以上算法，可以编写出下面的程序：

#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;
double f(double); //函数声明
double xpoint(double, double); //函数声明
double root(double, double); //函数声明
int main( )
{
double x1,x2,f1,f2,x;
do
{
cout<<"input x1,x2:";
cin>>x1>>x2;
f1=f(x1);
f2=f(x2);
} while(f1*f2>=0);
x=root(x1,x2);
cout<<setiosflags(ios::fixed)<<setprecision(7);
//指定输出7位小数
cout<<"A root of equation is "<<x<<endl;
return 0;
}
double f(double x) //定义f函数,以实现f(x)
{
double y;
y=x*x*x-5*x*x+16*x-80;
return y;
}
double xpoint(double x1, double x2) //定义xpoint函数,求出弦与x轴交点
{
double y;
y=(x1*f(x2)-x2*f(x1))/(f(x2)-f(x1)); //在xpoint函数中调用f函数
return y;
}
double root(double x1, double x2) //定义root函数,求近似根
{
double x,y,y1;
y1=f(x1);
do
{
x=xpoint(x1,x2); //在root函数中调用xpoint函数
y=f(x); //在root函数中调用f函数
if (y*y1>0)
{
y1=y;
x1=x;
}
else
x2=x;
}while(fabs(y)>=0.00001);
return x;
}

运行情况如下： input x1, x2:2.5 6.7↙ A root of equation is 5.0000000 对程序的说明： 1) 在定义函数时，函数名为f，xpoint和root的3个函数是互相独立的，并不互相从属。这3个函数均定为双精度型。 2) 3个函数的定义均出现在main函数之后，因此在main函数的前面对这3个函数作声明。习惯上把本程序中用到的所有函数集中放在最前面声明。 3) 程序从main函数开始执行。 4) 在root函数中要用到求绝对值的函数fabs，它是对双精度数求绝对值的系统函数。它属于数学函数库，故在文件开头用#include <cmath>把有关的头文件包含进来。

来源：未知/所属分类：基础教程/更新时间：2014-10-15 14:50

[返回列表]

顶一下

(0)

踩一下

(0)

上一篇：C++函数的默认参数

下一篇：C++函数的递归调用

C++函数的嵌套调用

最新内容

热点内容